Cookie Cutter Photometry

CCD Detectors

Older CCD detectors, also known as charged coupled devices, are composed of an array of pixels that function as light sensitive cells. The photoelectron effect causes these pixels to release electrons when struck by light, ultimately generating a charge proportional to the number of incoming photons. The term “counts” refers to the number of photons collected by each pixel and is related to the star’s brightness. Newer astrophotography detectors are made using semiconductors, which use a different type of physical process to produce counts per pixel.

While counts can be used to determine a star’s brightness, the number of photons lost on their journey from the star to the detector must first be considered. Even though the majority of photons emitted by a visible star do reach our atmosphere without too many collisions, sometimes the molecules in our atmosphere interact with these photons and cause refraction or absorption. This results in a reduction in the number of photons that reach ground based detectors. Furthermore, as the remaining photons pass through the telescope lens, some of them end up hitting the optical tube walls instead of the CCD. Because of this loss of photons detected, one must model all of these interactions in order to measure a star’s total brightness using counts.

Some follow the process described above to measure a star’s total brightness, but there is an alternative method commonly used that involves comparing the relative brightness of one star with another. To do this, astronomers divide the photon counts from the star of interest by the photon counts of another nearby bright star. This eliminates the need to consider photons lost due to refraction, absorption, and collisions since the light from both stars are assumably following a very similar path and experiencing the same loss of photons along the way.

It is also important to subtract the pixel counts that are caused by thermal properties of the CCD detector. Sometimes electrons that are produced by the CCD detector itself are collected by the pixels and included in the number of counts. These electrons are referred to as “dark currents” and will usually occur across all of the pixels in the detector. Because of this, we are able to remove this background noise by taking images with no light present (either a lens cap can be placed on the telescope or in GORT’s case, the dome closed) and an average counts per pixel is calculated. This average is then subtracted from astronomical images in order to remove any of these “false” counts. These false counts also need to be subtracted when measuring the relative brightness of stars unless the dark currents are uniform throughout the detector. The false counts surrounding each star should be calculated separately and subtracted from the respective star’s counts. Old-fashioned CCDs were uniform in their background noise. However, new detectors have variations in the dark current being produced across the pixels. That being said, the dark current is vastly reduced compared with older CCDs and dark calibration frames are not necessary for quality images.

The Astronomical Magnitude System

Astronomers measure the brightness of stars, galaxies, and even the sky itself using the “magnitude system.” Historically, the magnitude system is based on a concept first introduced by the Greek astronomer Hipparchus in about 129 B.C. Hipparchus produced the first well-known star catalog in the western world. In this catalog Hipparchus ranked stars by what he called “magnitude.” Since brighter stars tend to look bigger, Hipparchus called the brightest stars he could see those of the first magnitude. Stars not so bright he called second magnitude. Using this system he called the faintest stars he could just barely see sixth magnitude. This basic system has survived to the present time.

Galileo forced us to change this system slightly. When Galileo used a telescope to view the sky he discovered there were fainter stars. As Galileo expressed his finding…

“Indeed, with the glass, you will detect below stars of the sixth magnitude such a crowd of others that escape natural sight that it is hardly believable. … The largest of these… we may designate as of the seventh magnitude.” –Sidereus Nuncius, 1610

A new term was introduced (“seventh magnitude”) and the magnitude scale became open ended. As telescopes became bigger and better astronomers kept adding more magnitudes to the bottom of the scale.

By the middle of the 19th century astronomers realized it was necessary to define a more rigorous magnitude system. It had been determined that a 1st magnitude star was approximately 100 times brighter than a 6th magnitude star. Accordingly in 1856 Norman Poigson proposed that a difference of five magnitudes be defined as exactly a factor of 100 to 1. Since at this time in the western world it was believed that all human senses were logarithmic, it seemed perfectly reasonable to define a magnitude difference between two sources in the following manner…

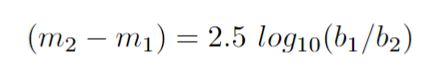
Here the bs are the amount of light from object 1 (the bright object) and 2 (the faint object). This gives the magnitude difference between the faint object and the bright object. Keep in mind that fainter objects will have larger magnitude numbers and brighter objects will have smaller magnitude numbers. (Very bright objects will even have negative magnitudes). This relationship became known as Poigson’s rule. This rule describes how brightness measured by some instrument sensitive to light can be represented as astronomical magnitudes.

It is particularly convenient (and even easy) to determine the magnitude of a star with respect to a nearby star for which the magnitude is known. That is, we can determine the magnitude difference between an unknown star and a reference star or standard star with a known magnitude. This type of magnitude determination is termed “differential photometry.” Of course, in the final analysis all magnitude determinations are differential since the stars themselves (or at least a set of standard stars) effectively determine the entire magnitude system. Here is a video explaining some of these same concepts.

Setting up the Project

Project Goals:

• Learn about how we subtract the background from a picture to get an accurate measurement of a stars brightness.

Materials for each participant:

• Clay model star field (modeling clay or Play-Doh)
• Plastic knife
• Pencil
• Triple beam balance or kitchen scale (for measuring mass)
• Ruler
• Paper plates
• Wax paper

Procedure:

1. Pre-class: Prepare the clay star field models for each group of participants. Have them read about CCD detectors for homework.
2. In class: Go over the vocabulary. (digital image, pixels, CCD, background, photometry, astronomical magnitudes). Stress that the clay models are representations of the light striking the detector. The thicker (or higher) the clay, the more light reached that particular part of the image. Also stress that virtually all astronomical measurements are relative (or differential) with respect to some known standard objects or sources. Discuss with the participants the concept of a pixellated detector. Also discuss the magnitude system, giving them examples of magnitudes of different objects in the sky. Have participants calculate a few magnitude differences given star brightness measurements (say, in number of electrons produced, of the volts produced
   by some detector). Instructors may need to help participants make a connection between the height of the clay model star fields and brightness. A good example would be topography maps for mountains.
3. Post-class: Look at some digital images of astronomical sources. Zoom in to see the pixels. Demonstrate the use of software used to analyze astronomical images.

Preparing the Clay Star Fields: A Teachers Guide

Option 1:
Instructor prepares the star field models. Be sure to record accurate masses of each star. For best results the mass of the clay or dough should be about:

• larger star ~40g
• smaller star ~15g
• background should weigh out to be ~155g

Start with three fingers of modeling clay. Flatten it out using a pencil, a rolling pin, or your fingers. Make the sheet about 6 inches by 6 inches and about 1/4 inch thick. The sheet does not need to be perfectly flat or smooth. Then take a strawberry sized piece of clay. Form this clay into a cone. Measure and record the mass of the cone so you know what to expect for results. Lightly press the cone onto the sheet with the flat side of the cone down. Take more clay, of a different size, and form another cone. The second cone should be either larger or smaller than the first cone. Measure and record the mass of the second cone. Lightly press this second cone onto the clay sheet. You now have a model star field with two stars. Of course, you could add another star or two if you wish.
Option 2:
Instructor prepares the cones that represent the stars. Learners prepare the clay sheet that represents the background brightness. Instructor then adds the stars.
Option 3:
Each pair of learners or learner team prepares a model star field. Learners then trade models with another team. Each learner team must record the measurements of their star field that they create for their classmates.

Post-Project

Activity Goals:
The goal is to determine the magnitude difference between two model stars. Learners must measure the mass of each model star. This includes determining how much mass is being contributed by the background and subtracting this background for the final results. The ratio of the masses for the model stars can then be used in the magnitude difference equation to compute a magnitude difference. If the masses of the star cones are measured before being placed on the clay sheets the true value for the magnitude difference that learners should obtain can be known in advance.

The learners are not allowed to simply pull or separate the stars from the flat surface. You must encourage the learners to figure out how to “subtract the background” from the star. One way of subtracting the the background from the star is by cutting out the star with the background attached from the flat piece. Learners can weigh this piece and then use it as a template to cut out a circle of the same size from the flat background piece. To get the weight of the star learners simply subtract the weight of the background circle from the weight of the star that has the background circle attached to it. This is very similar to how astronomers subtract a circle of the background from a circle that has background and a star in it.

Extension Activities: Extra Credit – Try in real life

1. Use binoculars or small telescopes to measure the brightness of some variable stars. The AAVSO provides excellent resources for such activities:
   http://aavso.org
2. Obtain digital images using a local telescope system with CCD detector. Local amateur astronomers often have telescopes and CCDs that could be used to obtain some images. It may be possible to arrange a demonstration of the equipment and to obtain some images. Local universities or colleges may also have astronomy programs and may be willing to provide demonstrations and images.

OR

1. Obtain digital images using a remote robotic telescope system. Several organizations maintain robotic telescope systems and allocate at least some time for educational purposes. Such organizations include the Global Telescope Network (GTN), Telescopes In Education (TIE), and Hands On Universe (HOU). Several companies and organizations maintain telescope systems, which may be reserved and used for a modest fee.
2. Analyze astronomical images to determine magnitudes for variable sources. University researchers and research organizations may have image data that learners could learn to reduce and analyze. Some organizations, such as the GTN, maintain image archives of variable objects that could be analyzed as learner projects.

Lesson Adaptations:
Visually impaired learners could touch the star model and describe what they feel.

Assessment:
To assess learner’s performance in this activity, collect the worksheets with their data measurements and calculations and check for completeness and correctness.

Background Correction

When making a measurement of a star’s brightness, we must be careful to correct for any other sources of light. These can contaminate the values of the star brightness. These sources include light from the sky and from the detector itself. Together these are called (for obvious reasons) “background counts.”

Even under the most ideal circumstances the sky is never truly black, that is, without any light. Of course, in an urban or even a suburban environment light pollution from artificial light sources will illuminate dust and molecules in the atmosphere. The atmosphere itself emits some light resulting from interactions of solar wind particles within the upper atmosphere. Another source is the integrated light from faint and distant stars. All of these sources from the sky are recorded by the detector, and are collectively called the “sky brightness.”

A final important source results from the detector itself. Even in the total absence of light a detector will produce electrons that get placed into the pixels. For an electronic detector this is termed “dark current.”

In order to accurately measure the brightness of a star, the observer must correct for these background counts. The “background annulus” formed by the inner and outer circles represents a region we can use to estimate the average background brightness reaching each pixel. This factor may be used to correct the pixel sum from the analysis aperture depending on the number of pixels in the analysis aperture.

In this exercise, you will determine a method of doing this by taking ruler and weight measurements, and then determine the brightness of a star using the magnitude system.